Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

Lý thuyết Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0° đến 180° – Chân trời sáng tạo

A. Lý thuyết

Bạn đang xem: Lý thuyết Giá trị lượng giác của một góc từ 0° đến 180° – Toán 10 Chân trời sáng tạo

1. Giá trị lượng giác

Mở rộng khái niệm tỉ số lượng giác cho các góc α từ 0° đến 180°, ta có định nghĩa sau đây: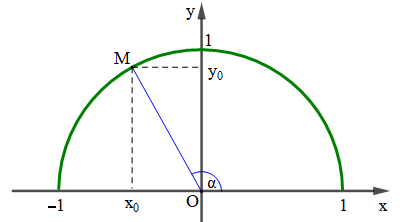

Với mỗi góc α (0° ≤ α ≤ 180°), ta có thể tìm được một điểm M trên nửa đường tròn đơn vị sao cho xOM^=α. Gọi (x0; y0) là tọa độ của điểm M, ta có:

– Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0;

– Hoành độ x0 của M là cosin của góc α, kí hiệu là cosα = x0;

– Tỉ số y0/x0 (x0 ≠ 0) là tang của góc α, kí hiệu là tanα=y0/x0;

– Tỉ số x0/y0 (y0 ≠ 0) là cộtang của góc α, kí hiệu là cotα=x0/y0;

Các số sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của góc α.

Ví dụ 1. Tìm các giá trị lượng giác của góc 150°.

Hướng dẫn giải

Lấy điểm M trên nửa đường tròn đơn vị sao cho xOM^=150°.

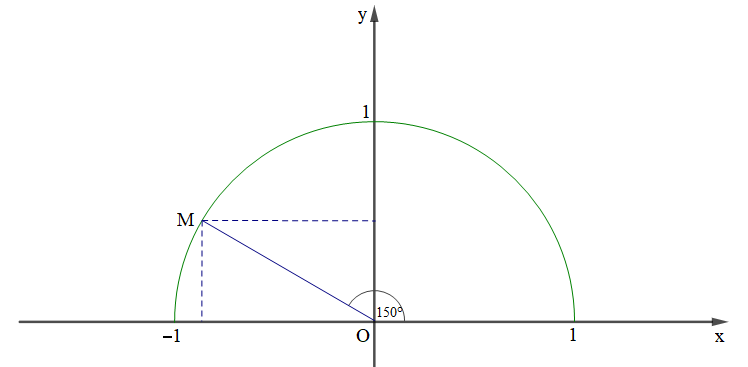Ta có MOy^=150°−90°=60°.

Khi đó ta tính được tọa độ của điểm M là −32;12.

Xem thêm : No sooner là gì? Kiến thức chung về cấu trúc No sooner trong tiếng Anh

Theo định nghĩa ta có:

sin150°=12; cos150°=−32; tan150°=−13; cot150°=−3.

Chú ý:

a) Nếu α là góc nhọn thì các giá trị lượng giác của α đều dương.

Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.

b) tanα chỉ xác định khi α ≠ 90°.

cotα chỉ xác định khi α ≠ 0° và α ≠ 180°.

Ví dụ 2. Với α = 30° thì sinα > 0, cosα > 0, tanα > 0 và cotα > 0.

Với α = 150° (như trong Ví dụ 1) thì sinα > 0, cosα < 0, tanα < 0 và cotα < 0.

2. Quan hệ giữa các giá trị lượng giác của hai góc bù nhau

Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có:

sin(180° ‒ α) = sinα;

cos(180° ‒ α) = ‒cosα;

tan(180° ‒ α) = ‒tanα (α ≠ 90°);

cot(180° ‒ α) = ‒cotα (0° < α < 180°).

Xem thêm : Văn mẫu lớp 11: Phân tích bài Văn tế nghĩa sĩ Cần Giuộc 2 Dàn ý & 12 bài văn mẫu hay nhất

Ví dụ 3.

a) Biết sin60°=1/2. Tính cos30°, cos150°, sin120°.

b) Biết tan45° = 1. Tính tan135°.

Hướng dẫn giải

a) Ta có: sin60°=1/2

Suy ra:

cos30°=cos90°−60°=sin60°=1/2 (vì 30° và 60° là hai góc phụ nhau)cos150°=cos180°−30°=−cos30°=−1/2 (vì 150° và 30° là hai góc bù nhau)sin120°=sin180°−60°=sin60°=1/2 (vì 120° và 60° là hai góc bù nhau);

b) Ta có: tan45° = 1.

Suy ra:

tan135° = tan(180° ‒ 45°) = ‒tan45° = ‒1 (vì 135° và 45° là hai góc bù nhau);

3. Giá trị lượng giác của một số góc đặc biệt

Dưới đây là bảng giá trị lượng giác của một số góc đặc biệt:

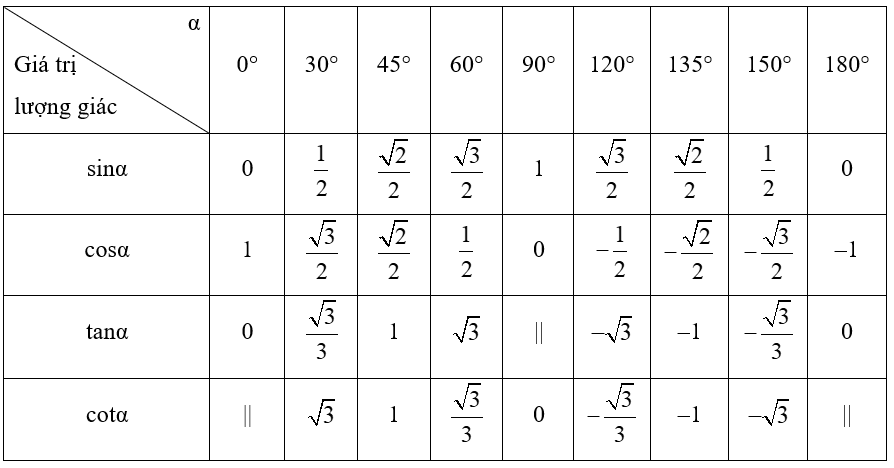Chú ý: Trong bảng, kí hiệu “||” để chỉ giá trị lượng giác không xác định.

Ví dụ 4. Tính giá trị các biểu thức sau:

a) A = a^2.sin90° + b^2.cos90° + c^2.cos180°;

b) B = 3 – sin2135° + 2cos2120° ‒ 3tan2150°.

Nguồn: https://toibiet.net
Danh mục: Giáo Dục