Lý thuyết hàm số lũy thừa

1. Định nghĩa của hàm số mũ

Hàm số mũ là các hàm số có dạng (y = {x^alpha }left( {alpha in R} right)). Các hàm số mũ có các tập xác định khác nhau, phụ thuộc vào (alpha):

Bạn đang xem: Lý thuyết hàm số lũy thừa

• Nếu (alpha) là số nguyên dương, thì tập xác định là (R).
• Nếu (alpha) là số nguyên âm hoặc (alpha = 0), thì tập xác định là (Rbackslash left{ 0 right}).
• Nếu (alpha) không phải số nguyên, thì tập xác định là (left( {0; + infty } right)).

Lưu ý: Hàm số (y = căn bậc hai của x) có tập xác định là (left[ {0; + infty } right)), hàm số (y = căn bậc ba của x) có tập xác định là (R), trong khi các hàm số (y = {x^{frac{1}{2}}}, y = {x^{frac{1}{3}}}) có cùng tập xác định là ((0; + infty )). Do đó, (y = căn bậc hai của x ) và (y = {x^{frac{1}{2}}}) (hoặc (y = căn bậc ba của x) và (y = {x^{frac{1}{3}}})) là hai hàm số khác nhau.

2. Đạo hàm của hàm số mũ với số mũ tổng quát

– Hàm số (y = {x^alpha }) có đạo hàm tại mọi (x ∈ (0; + infty )) và (y’ = left( {{x^alpha }} right)’ = alpha {x^{alpha – 1}}).

– Nếu hàm số (u = u(x)) có giá trị dương và có đạo hàm trong khoảng (J), thì hàm số (y = {u^alpha }left( x right)) cũng có đạo hàm trên (J) và [y’ = left[ {{u^alpha }left( x right)} right]’ = alpha {u^{alpha – 1}}left( x right)u’left( x right)]

3. Đạo hàm của hàm số mũ với số mũ nguyên dương

Xem thêm : Thuyết minh về địa đạo Củ Chi – Địa danh lịch sử

Trong trường hợp số mũ là số nguyên dương, hàm số mũ (y = x^n) có tập xác định là (R) và có đạo hàm trên toàn trục số. Công thức tính đạo hàm của hàm số mũ tổng quát được mở rộng thành (forall x in R, left( {{x^n}} right)’ = n{x^{n – 1}}) và [forall x in J,left[ {{u^n}left( x right)} right]’ = n{u^{n – 1}}left( x right)u’left( x right)]]nếu (u = u(x) ) có đạo hàm trong khoảng (J).

4. Đạo hàm của hàm số mũ với số mũ nguyên âm

Trong trường hợp số mũ là số nguyên âm, hàm số mũ (y = x^n) có tập xác định là (Rbackslash left{ 0 right}) và có đạo hàm tại mọi (x) khác (0). Công thức tính đạo hàm của hàm số mũ tổng quát được mở rộng thành (forall x ne 0, left( {{x^n}} right)’ = n{x^{n – 1}}) và [forall x in J, left[ {{u^n}left( x right)} right]’ = n{u^{n – 1}}left( x right)u’left( x right)]], nếu (u= u(x) ne 0) có đạo hàm trong khoảng (J).

5. Đạo hàm của căn thức

Hàm số (y = căn bậc n của x) có thể xem là mở rộng của hàm số mũ (y = {x^{frac{1}{n}}}) (tập xác định của (y = căn bậc n của x) chứa tập xác định của (y = {x^{frac{1}{n}}}) và trên tập xác định của (y = {x^{frac{1}{n}}}), hai hàm số này trùng nhau).

Khi (n) là số lẻ, hàm số (y = căn bậc n của x) có tập xác định là (R). Trên khoảng ((0; + infty) ), ta có (y = căn bậc n của x = {x^{frac{1}{n}}}) và (left( {{x^{frac{1}{n}}}} right)’ = dfrac{1}{n}{x^{frac{1}{n} – 1}}), do đó (left( {căn bậc n của x } right)’ = dfrac{1}{{ncăn bậc n {{{x^{n – 1}}}}}}).

Công thức này cũng đúng với (x < 0) và hàm số (y = căn bậc n của x) không có đạo hàm tại (x = 0).

Khi (n) là số chẵn, hàm số (y = căn bậc n của x) có tập xác định là ([0;+ infty)), không có đạo hàm tại (x = 0) và có đạo hàm tại mọi (x > 0) tính theo công thức:

Xem thêm : TOP 8 bài Thuyết minh bài Phú Sông Bạch Đằng của Trương Hán Siêu Hay chọn lọc

[left( {căn bậc n của x } right)’ = dfrac{1}{{ncăn bậc n {{{x^{n – 1}}}}}}]

Tóm lại, ta có (left( {căn bậc n của x } right)’ = dfrac{1}{{ncăn bậc n {{{x^{n – 1}}}}}}) đúng với mọi (x) làm cho cả hai vế có ý nghĩa.

Sử dụng quy tắc đạo hàm hàm hợp, ta suy ra: Nếu (u = u(x)) là hàm có đạo hàm trong khoảng (J) và thoả mãn điều kiện (u(x) > 0, ∀x ∈ J) khi (n) chẵn, (u left( x right) ne 0,forall x in J) khi (n) lẻ, thì [forall x in J,left( {căn bậc n của {u left( x right)}} right)’ = dfrac{{u’left( x right)}}{{ncăn bậc n {{{u^{n – 1}}left( x right)}}}}]

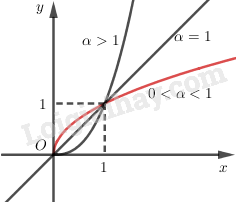
6. Đồ thị của hàm số (y = {x^alpha }) trên khoảng ((0; + infty))

Lưu ý: Khi nghiên cứu hàm số (y = {x^alpha }) với (alpha) cụ thể, cần xét hàm số trên toàn tập xác định của nó (không chỉ trên khoảng ((0; + infty)) như ở trên).

Loigiaihay.com

Nguồn: https://toibiet.net
Danh mục: Giáo Dục