Lý thuyết phương trình mặt phẳng

1. Định nghĩa và tính chất của vectơ pháp tuyến của mặt phẳng

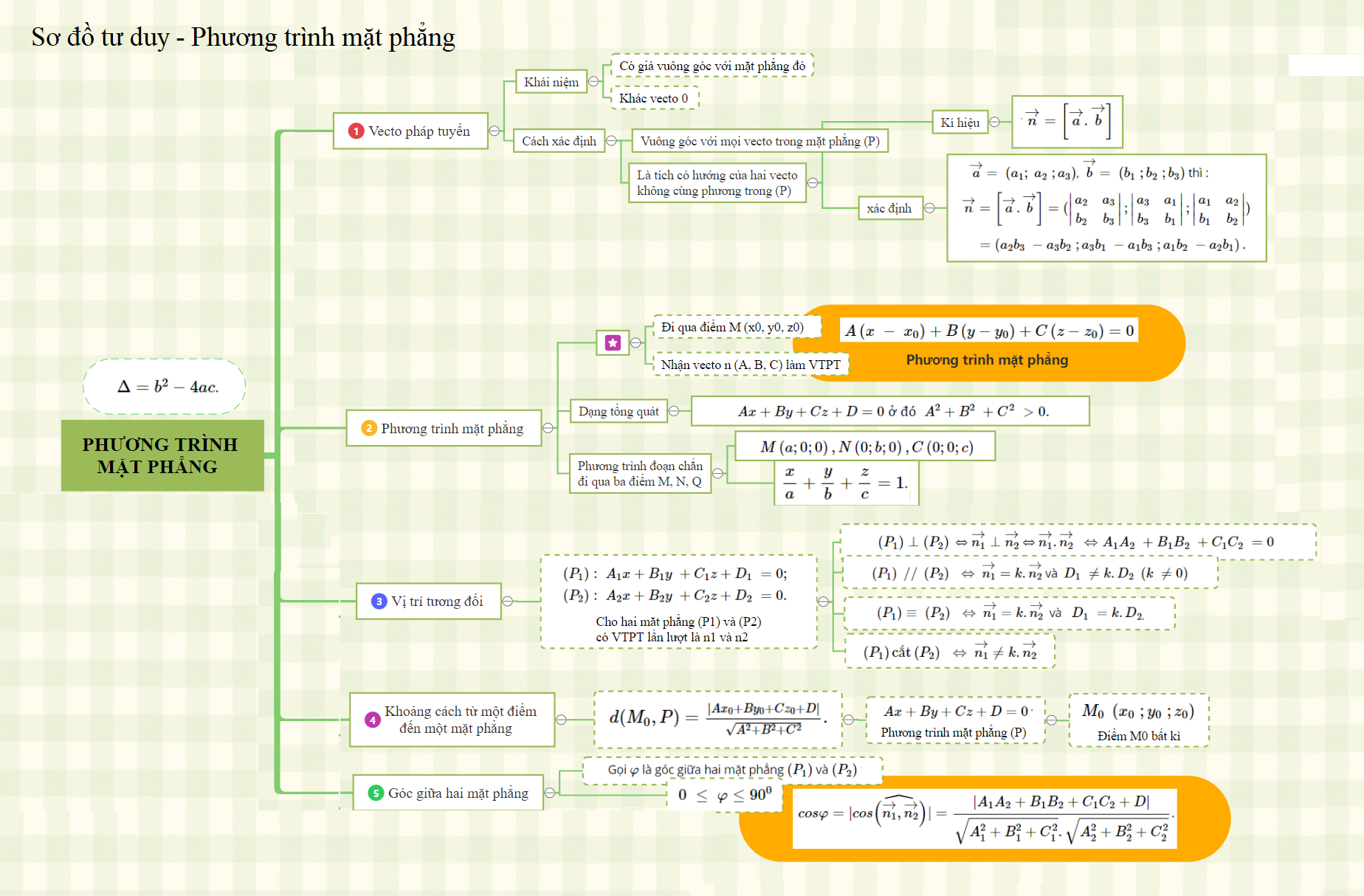
* Đối với một mặt phẳng ((P)), vectơ (overrightarrow{n} ≠ overrightarrow{0}) mà vuông góc với mặt phẳng ((P)) được gọi là vectơ pháp tuyến của mặt phẳng.

Bạn đang xem: Lý thuyết phương trình mặt phẳng

* Đối với một mặt phẳng ((P)), cặp vectơ (overrightarrow{a} ≠ overrightarrow{0}), (overrightarrow{b} ≠ overrightarrow{0}) mà không cùng phương và nằm trong mặt phẳng ((P)) được gọi là cặp vectơ chỉ phương của mặt phẳng ((P)). Khi đó, vectơ (overrightarrow{n} = [overrightarrow{a}.overrightarrow{b}]) là vectơ pháp tuyến của mặt phẳng ((P)).

* Nếu (overrightarrow{a}) ( = (a_1, a_2, a_3)) và (overrightarrow{b}) ( = (b_1, b_2, b_3)) thì:

        (overrightarrow{n} = [overrightarrow{a}.overrightarrow{b}] = (|2b_3 – 3a_3|, |3a_3 – b_2|, |a_2 – 2b_1|))

        ( = (2b_3 – 3a_3, 3a_3 – b_2, a_2 – 2b_1))

* Một mặt phẳng được xác định hoàn toàn bởi một điểm và một vectơ pháp tuyến của nó, hoặc một điểm thuộc mặt phẳng và một cặp vectơ chỉ phương của nó.

2. Phương trình mặt phẳng

* Mặt phẳng ((P)) đi qua điểm (M_0 = (x_0, y_0, z_0)) và có vectơ pháp tuyến (A, B, C) có phương trình dạng: (A(x – x_0) + B(y – y_0) + C(z – z_0) = 0)

* Mọi mặt phẳng trong không gian có phương trình tổng quát dạng:

Xem thêm : Biến đổi đơn giản biểu thức chứa căn bậc hai – Cùng Toppy chia sẻ

        (Ax + By + Cz + D = 0, với A^2 + B^2 + C^2 > 0).

        Trong đó, vectơ (n(A, B, C)) là vectơ pháp tuyến của mặt phẳng.

* Mặt phẳng đi qua ba điểm (M(a, 0, 0), N(0, b, 0), C(0, 0, c)) với (abc ≠ 0) có phương trình: (x/a + y/b + z/c = 1). Phương trình này còn được gọi là phương trình mặt phẳng theo đoạn chắn.

3. Vị trí tương đối của hai mặt phẳng

Cho hai mặt phẳng (P_1) và (P_2) có phương trình:

        ((P_1): A_1x + B_1y + C_1z + D_1 = 0), ((P_2): A_2x + B_2y + C_2z + D_2 = 0)

Đặt (overrightarrow{n_1} = (A_1, B_1, C_1) tương ứng với (P_1)) và (overrightarrow{n_2} = (A_2, B_2, C_2) tương ứng với (P_2)). Khi đó:

        ((P_1) // (P_2) ⇔ (overrightarrow{n_{1}} trương đồng với overrightarrow{n_{2}}) ⇔ (overrightarrow{n_{1}}.overrightarrow{n_{2}};) ( = 0)

        ( (P_1) cắt (P_2) ⇔ (overrightarrow{n_{1}} không trương đồng với overrightarrow{n_{2}}) (nghĩa là (overrightarrow{n_{1}}) và (overrightarrow{n_{2}}) không cùng phương).

4. Khoảng cách từ một điểm đến một mặt phẳng

Xem thêm : Phép Quay: Lý Thuyết, Công Thức Và Các Dạng Bài Tập | Toán 11

Trong không gian (Oxyz), cho mặt phẳng ((P)) có phương trình:

        (Ax + By + Cz + D = 0) và điểm (M_0 = (x_0, y_0, z_0)). Khoảng cách từ M_0 đến ((P)) được tính bằng công thức:

        (d(M_0, P) = frac{}{{sqrt {{A^2 + B^2 + C^2}} }}).

5. Góc giữa hai mặt phẳng

Cho hai mặt phẳng ((P_1)) và ((P_2)) có phương trình:

        ((P_1): A_1x + B_1y + C_1z + D_1 = 0), ((P_2): A_2x + B_2y + C_2z + D_2 = 0)

Gọi (varphi) là góc giữa hai mặt phẳng ((P_1)) và ((P_2)) thì (0 ≤ varphi ≤ 90°) và:

        (cosvarphi =|coswidehat{(overrightarrow{n_{1}},overrightarrow{n_{2}})}|=frac{{|A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}+D|}}{{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}} ).

Loigiaihay.com

Nguồn: https://toibiet.net
Danh mục: Giáo Dục